How to Convert Decimal to Binary | Methods and Examples

What Are Binary Numbers?

Think about phone numbers, zip codes, money, measures, or even time. They are all basically numbers 0 to 9, aren’t they? To be precise, they use the decimal number system or the base-10 numerals.

But, what’s especially interesting about the language of computers is that it uses the binary number system. A binary number is made of 0s and 1s. A binary digit is called a bit.

In this lesson, we are going to show you two different methods of converting a decimal number into a binary number.

Converting Decimal to Binary Using the Sum-of-Weights Method

As there are powers of 10 to represent the value of each place of a decimal number, there are powers of 2 to denote the weight of each bit of a binary number. In the sum-of-weights method, we decompose the decimal number into the sum of powers of 2 and figure out the binary equivalent. Let’s understand the steps by converting the decimal number 25 into a binary number.

Step 1: Look for a power of 2 that is less than or equal to the decimal number.

Let’s write down the powers of 2.

Now, 32 > 25 so we go with 2⁴ = 16.

Step 2: Decompose the decimal number with the chosen power of 2 as one of the addends.

Let’s decompose 25 with 16 as one of the addends.

25 = 16 + 9

Note: To find the other addend, subtract the selected power of 2 from the given decimal number. In the above equation, when we subtract 16 from 25, we get 9.

Step 3: Repeat the steps 1 and 2 until all the addends are powers of 2.

Now, we need to decompose 9. 2³ = 8 is the highest power that’s less than or equal to 9. So, we have:

9 = 8 + 1

Here, both the addends are powers of 2. So, we stop.

Step 4: Express the decimal number as the sum of weights.

We have decomposed our decimal number as:

25 = 16 + 8 + 1

Expressing it as the sum of powers of 2 or the sum of weights, we have:

25 = 2⁴ + 2³ + 2⁰

Step 5: Assign 1 to the powers of 2 we've used to decompose the number and 0 to the others.

Let’s make a table with the weights 2⁴ to 2⁰ as columns.

As you can see, we have assigned 1s to 2⁴, 2³, and 2⁰, and 0s to 2¹ and 2².

Step 6: The string of 0s and 1s from left to right is the required binary equivalent.

Here, the binary equivalent of 25 is 11001. Thus, we have:

(25)₁₀ = (11001)₂

Note: The subscripts 10 and 2 indicate the numbers in base 10 and base 2 respectively.

Let’s look at another example for the same conversion.

Example

Convert 106 from base-10 to base-2.

Listing the powers of 2, we have:

Here 128 > 106; so let's select 2⁶ = 64.

Decomposing 106, we have:

Composing the string of 0s and 1s, we have:

Therefore, the required binary equivalent of 106 is 1101010.

⇨ (106)₁₀ = (1101010)₂

Converting Decimal to Binary Using the Double-Dabble Method

The double dabble method or the repeated division method is the easiest way to convert a decimal number into a binary number. Let’s convert 115 from base 10 to base 2 using repeated division.

Step 1: Perform repeated division of the decimal number by 2 until you obtain 1 as the quotient. Keep track of the remainders in each step.

Check out the double-dabble method for 115 with a click on the number!

Step 2: Write the final quotient 1 along with the remainders from the bottom to the top, and compose the binary string.

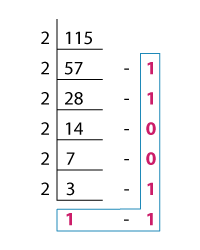
⇨ (115)₁₀ = (1110011)₂

It’s Your Turn Now!

Convert 145₁₀ to a binary number using the double-dabble method.

Hide answer

View answer

A Few Points to Ponder

• A binary number comprises 0s and 1s and is written with a subscript 2.

• A binary digit is called a bit. The weight of each bit is represented in powers of 2.

• Every decimal number has a unique binary equivalent.

• To convert a decimal to binary, we use either the sum-of-weights method or the double-dabble method.