Divisibility Rules for 2, 3, 4, 5, 6, 7, 8, 9 & 10 | Handy Tricks
- Math Lessons >
- Divisibility Rules
Overview of Divisibility Rules:
- What Are Divisibility Rules?
- Divisibility Rules - Video Lesson
- Divisibility Rule for 2
- Divisibility Rule for 3
- Divisibility Rule for 4
- Divisibility Rule for 5
- Divisibility Rule for 6
- Divisibility Rule for 7
- Divisibility Rule for 8
- Divisibility Rule for 9
- Divisibility Rule for 10
- Lighten it Up with Some Number - Finding Fun
- Interesting Facts
- The Lesson in a Nutshell
- Divisibility Rules - Quiz
What Are Divisibility Rules?
Divisibility rules are simple tests that help decide whether or not a number is divided by another number evenly and without performing the usual calculations.
Take a look at this scenario:
Aaron picks 568 apples from his orchard. He has only six cartons. Will Aaron be able to pack the apples evenly in the six cartons with no leftovers?

To solve a problem like this, ideally we would divide the number of apples by 6. But with divisibility rules at your fingertips, you can answer it easily without doing too much calculation.
In this lesson, we’ll walk you through the divisibility rules for numbers 2 through 10 and illustrate the concept with relevant examples.
Divisibility Rule for 2
All even numbers are divisible by 2. So, look for numbers that have 0, 2, 4, 6, or 8 as their last digit.
Examples
Is 286 divisible by 2?
TestThe number 286 has 6 as its last digit.
Result286 is divisible by 2.
Is 3,527 divisible by 2?
TestThe last digit here, 7, is an odd number.
Result3,527 is not divisible by 2.
Divisibility Rule for 3
Add up all the digits, and divide the sum by 3. If there are no remainders, the number will pass the divisibility test for 3.
Examples
Is 618 divisible by 3?
TestThe sum of the digits is:
6 + 1 + 8 = 15.
15 is a multiple of 3. (3 x 5 = 15)
Result618 is divisible by 3.
Is 1,369 divisible by 3?
TestThe sum of the digits is:
1 + 3 + 6 + 9 = 19.
Dividing 19 by 3,
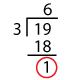
We have 1 left over.
Result1,369 is not divisible by 3.
Divisibility Rule for 4
Pick the last two digits, and divide the number formed by 4. If there’s no remainder, the number is divisible by 4.
Examples
Is 778 divisible by 4?
TestThe number formed by the last two digits is 78.
Dividing 78 by 4,
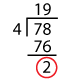
We are left with 2 as the remainder.
Result778 is not divisible by 4.
Is 12,456 divisible by 4?
TestThe number formed by the last two digits is 56.
Dividing 56 by 4,
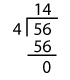
We have nothing left over.
Result12,456 is divisible by 4.
Divisibility Rule for 5
A number is divisible by 5 if it has 0 or 5 in its ones place.
Examples
Is 154 divisible by 5?
TestThe number has 4 in the ones place.
Result154 is not divisible by 5.
Is 66,505 divisible by 5?
TestThe number ends in 5.
Result66,505 is divisible by 5.
Divisibility Rule for 6
If a number is divisible by 2 and 3, it is divisible by 6 as well.
A Venn diagram can really come handy to understand this rule.
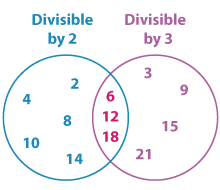
As you can see the numbers 6, 12, and 18 in the intersection are divisible by both 2 and 3. Thus, they are divisible by 6 as well.
Examples
Is 7,284 divisible by 6?
TestThe last digit is 4.
⇨ 7,284 is divisible by 2.
The sum of the digits is:
7 + 2 + 8 + 4 = 21.
21 is a multiple of 3. (3 x 7 = 21)
⇨ 7,284 is divisible by 3.
Result7,284 is divisible by 6.
Is 14,348 divisible by 6?
TestThe number is even with 8 as its last digit.
⇨ 14,348 is divisible by 2.
The sum of the digits is:
1 + 4 + 3 + 4 + 8 = 20.
Dividing 20 by 3,
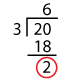
We have 2 as the remainder.
⇨ 14,348 is not divisible by 3.
Result14,348 is not divisible by 6.
Divisibility Rule for 7
Double the last digit and subtract it from the number formed by the other digits. If the difference is divisible by 7, the number is divisible by 7, too.
Examples
Is 644 divisible by 7?
TestDoubling the last digit, we have 4 x 2 = 8.
The number formed by the other digits is 64.
Now, 64 – 8 = 56.
56 is a multiple of 7. ( 7 x 8 = 56)
Result644 is divisible by 7.
Is 3,876 divisible by 7?
TestDoubling the last digit, we have 6 x 2 = 12.
The number formed by other digits is 387.
Now, 387 – 12 = 375.
Let’s repeat the process.
Doubling the last digit 5 gives us 10.
The number formed by other digits is 37.
37 – 10 = 27.
Dividing 27 by 7,
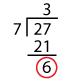
We are left with 6 as the remainder.
Result3,876 is not divisible by 7.
Divisibility Rule for 8
If the number formed by the last three digits is divisible by 8, the number is divisible by 8.
Examples
Is 28,256 divisible by 8?
TestThe number formed by the last three digits is 256.
Dividing 256 by 8,
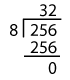
256 leaves no remainder when divided by 8.
Result28,256 is divisible by 8.
Is 786,874 divisible by 8?
TestThe number formed by the last three digits is 874.
Dividing 874 by 8,
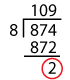
It leaves a remainder, 2.
Result786,874 is not divisible by 8.
Divisibility Rule for 9
Add up all the digits and divide the sum by 9. If the sum is divisible by 9, the number is divisible by 9, too. Alternatively, you can repeat adding the digits until you end up with 9.
Examples
Is 65,547 divisible by 9?
TestAdding all the digits, we have:
6 + 5 + 5 + 4 + 7 = 27.
27 is divisible by 9.
Also, adding the digits 2 and 7, we get 9.
Result65,547 is divisible by 9.
Is 223,567 divisible by 9?
TestThe sum of the digits is:
2 + 2 + 3 + 5 + 6 + 7 = 25.
Repeating the process, we have 2 + 5 = 7 instead of 9.
Result223,567 is not divisible by 9.
Note: The rule for 9 is similar to the rule for 3.
Divisibility Rule for 10
A number is divisible by 10 if it has zero as its last digit.
Examples
Is 89,340 divisible by 10?
TestThe number has 0 as the last digit.
Result89,340 is divisible by 10.
Is 7,654 divisible by 10?
TestThe number ends in 4 and not zero.
Result7,654 is not divisible by 10.
Lighten it Up with Some Number-Finding Fun
Here’s a simple number trick that uses the divisibility rules.
All you need to do is simply follow the instructions, and we’ll find the number on your mind.
Think of any natural number.
Double it and multiply by 5.
Now, the number you had in your mind is simply the product without the last digit.
Intrigued about the math that helped us amuse you? Click here!
Here, you are asked to double the number and multiply it by 5, which makes it divisible by 2 and 5.
When a number is divisible by 2 and 5, the product is divisible by 10.
So we simply ignore the zero at the end of the product, and the number is unveiled.
What are you waiting for? Play it on your friends and leave them awestruck!
Interesting Facts
A number divisible by 8 is divisible by 4 and 2. Similarly, a number divisible by 9 is divisible by 3.
Numbers that have two zeros at the end are divisible by 4. Numbers with three zeros at the end are divisible by 8.
A number divisible by 10 is divisible by 2 and 5.
The sum of 3 consecutive numbers is divisible by 3.
The number 2,520 is the smallest number that is divisible by 2, 3, 4, 5, 6, 7, 8, 9, and 10. Can’t quite believe it? Check for yourself!
The Lesson in a Nutshell
The result must be divisible by 7.

