Learn Equivalent Fractions with Visual Models and Examples

What Are Equivalent Fractions?

Equivalent fractions are fractions that refer to the same part of the whole. Look at this pizza:

It is first cut into two equal halves, then into 4 large slices, and finally into 8 perfect slices. Let's analyze each slicing.

Now, let’s assume that half of the pizza was eaten. What remains in each case would be:

The fractions 12, 24, and 48 have different numerators and denominators, but they all denote the same quantity or proportion of the pizza. This implies:

12 = 24 = 48

These are equivalent fractions.

Equivalent Fractions on a Number Line

Let’s represent the same equivalent fractions, which we started our discussion with, on a number line. Let’s divide the number line interval with respect to each denominator and plot the fractions.

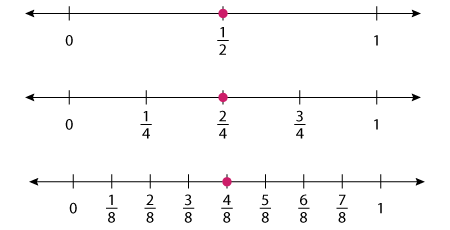
When you observe the above number lines carefully, you can find that each of the equivalent fractions is at the same distance from 0. This clarifies that equivalent fractions represent the same point on a number line. Now that we know what equivalent fractions are, let's generate some.

How to Generate Equivalent Fractions

Let’s get our heads around creating equivalent fractions. Let’s try generating a few equivalent fractions using this rectangular chocolate bar:

We'll break this chocolate bar vertically into three equal parts as shown.

Now we'll divide the bar between Sandra and Barbara as follows:

If we break the chocolate bar into two again, then Sandra’s and Barbara’s shares are:

Now breaking horizontally, their shares will be:

If you observe the fractions carefully, you’ll notice that the quantity of the chocolate bar each got has remained unchanged.

Thus, we’ve created equivalent fractions to represent their shares.

Are Models the Only Way to Generate Equivalent Fractions?

Of course not! An infinite number of equivalent fractions can be generated by multiplying the numerator and denominator by the same number. You can also generate equivalent fractions by dividing the numerator and denominator by a common factor. Here we have demonstrated how each method works.

How to Find Equivalent Fractions Using Multiplication

Let’s generate two equivalent fractions for 34.

First we'll multiply the numerator and denominator by 2.

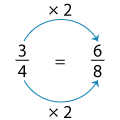
Here, 68 is equivalent to 34.

We'll find the next equivalent fraction by multiplying the numerator and denominator by 3 this time.

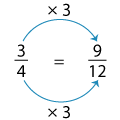
And that is our next equivalent fraction. So,

34 = 68 = 912.

Alternatively, you can generate equivalent fractions by multiplying the numerator and denominator of the product obtained as shown:

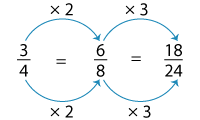
⇒ 34 = 68 = 912 = 1824

You can generate an endless list of equivalent fractions by multiplication!

How to Find Equivalent Fractions Using Division

Let’s try generating equivalent fractions for 3045.

Are there any common factors for the numerator and denominator?

To figure this out, we need to use the divisibility rules. In this case, 30 and 45 have the factors 3 and 5 in common. So, let’s proceed with division.

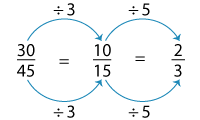
We can’t divide any further, so we stop with 23.

What happens when we change the order we choose the common factors?

Let’s divide by 5 first and 3 next.

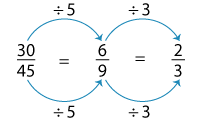
We’ve got another equivalent fraction 69. Thus, we have three fractions that are equivalent to 3045.

3045 = 1015 = 69 = 23.

Note: If you multiply or divide the numerator by any number, you should multiply or divide the denominator by the same number so the value of the fraction doesn’t change.

Example 1

Generate three equivalent fractions for 37.

Multiplying the numerator and denominator by 2, we get:

37 x 22 = 614.

Multiplying the numerator and denominator by 3, we get:

37 x 33 = 921.

Multiplying the numerator and denominator by 4, we get:

37 x 44 = 1228.

Thus, 37 = 614 = 921 = 1228.

Example 2

Complete this fraction-equivalence sentence replacing x with its value: 7x = 2133.

According to the definition, if two fractions are equivalent, we can say that the numerator and denominator of one fraction are multiplied or divided by a number so we get the other fraction.

In this case, 7x and 2133 are equivalent. So, we can rightly say:

7x x = 2133

Now, how many times 7 equals 21?

 ⇨ 217 = 3.

Thus, our equation becomes: 7x x 33 = 2133

Now, which number when 3 times gives 33?

 ⇨ 333 = 11

 ⇨ x = 11

∴ The complete fraction equivalence statement is 711 = 2133.

Understand Fraction Equivalence with the Fraction Bars!

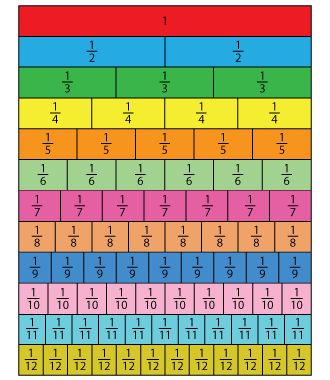
Look at the size of each tile and study what other tiles are equivalent to that size.

For instance, two 12 tiles equal 1 tile. Four 14 tiles also equal 1 tile.

⇒ 1 = 22 = 33 = 44 = 55 = 66 = 77 = 88 = 99 = 1010 = 1111 = 1212

It’s Your Turn Now!

1) Study the fraction strips and find the fraction equivalent to 36.

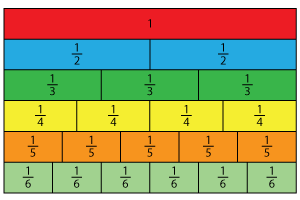
According to the fraction strips, 12 = 36.

Hide answer

View answer

2) Write five fractions that are equivalent to 512.

The equivalent-fraction sentence with five equivalents for 512 is:

512 = 1024 = 1536 = 2048 = 2560 = 3072.

Hide answer

View answer

3) Find x and y; complete this fraction-equivalence statement.

23 = 4x = y12.

x = 6, y = 8.

The complete statement is 23 = 46 = 812.

Hide answer

View answer

How to Check If the Fractions Are Equivalent

There’s a simple test to check whether two fractions are equivalent or not. All we need to do is reduce each fraction to its simplest form. If we end up with the same results, the fractions are equivalent. Here’s an example:

Let’s check out if 820 and 25 are equivalent.

We know that the fraction 25 is in its simplest form. We can’t reduce it any further. But, the fraction 820 can be written as:

820 = 2 x 2 x 22 x 2 x 5   [Factoring 8 and 20]

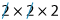
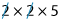  =   [Canceling the common factors]

  = 25.

This is a fraction that’s the same as the other fraction.

Therefore, the fractions are equivalent.

Here’s a Shortcut to Check Fraction Equivalence!

Let’s check if 224 and 24 are equivalent.

This time we’ll cross-multiply.

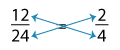
48 = 48.

We have 48 on both sides. This proves the two fractions are equivalent.

Summing Up!

• Equivalent fractions name the same part or proportion of a whole.

• A fraction can have an infinite number of equivalent fractions.

• Equivalent fractions denote the same point on the number line.

• Equivalent fractions reduce to the same simplest form.

• To generate a fraction that’s equivalent to another fraction, multiply or divide the numerator and denominator by the same number.

• To check if two fractions are equivalent:

•  ✯ Cancel out the common factors and reduce each fraction to its simplest form. If the simplest forms are the same, the fractions are equivalent.

• Or

•  ✯ Equate the fractions, cross multiply the numerator and denominator, and simplify the products. If you end up with the same results on both sides, then the fractions are equivalent.

---