How to Solve Multi-Step Inequalities

The very name “multi-step inequalities” explains that there are multiple steps and various properties that we need to apply in the process of arriving at their solutions. In this lesson, we are going to give you step-by-step instructions on how to solve multi-step inequalities in one variable – with the help of examples.

Solving Multi-Step Inequalities: A Step-by-Step Approach

Let's look at the steps one by one.

✯ Combine like terms if any and simplify each side of the inequality.

✯ Isolate the variable using the inverse operations. Reverse the sign when multiplying or dividing by a negative number.

✯ Solve for the variable.

Let’s deep dive into the process!

Solving Multi-Step Inequalities with Variables on One Side

Take this inequality for instance: 7 (3x + 2) < 56. Multiplication and addition are part of the inequality. Let’s follow the steps below and solve it:

Applying the distributive property to the inequality, we have:

 ⇨ 21x + 14 < 56

Now, the inverse operation of addition is subtraction. The subtraction property of inequality states that the inequality remains unchanged when you subtract the same number from both sides. So, let’s subtract 14 from each side.

 ⇨ 21x + 14 – 14 < 56 – 14

 ⇨ 21x < 42

To isolate the variable, we must perform the inverse operation of multiplication – division. The division property of inequality states that the inequality stays the same when you divide both sides by the same positive number whereas the symbol reverses when you divide by a negative number. Here we need to divide both sides by 21.

 ⇨ 21x21 < 4221

Canceling the common factors, we have:

 ⇨ x < 2

Thus, x can be any value less than 2.

A graphical representation of the solution would be:

Note: The value 2 is plotted with an open circle since it is not included in the solution set.

Let’s look at solving another inequality: z(–6) – 2 ≤ 1.

The inequality involves subtraction and division, so we need to perform the inverse operations: addition and multiplication respectively.

The addition property of inequality states that when we add the same number to both sides of the inequality, the inequality remains unchanged. Adding 2 to both sides, we have:

 ⇨ z(–6) – 2 + 2 ≤ 1 + 2

 ⇨ z(–6) ≤ 3

Now to isolate the variable, we need to perform multiplication, which is the inverse operation of division. The multiplication property of the inequality says that when we multiply both sides by the same positive integer, the inequality remains the same and when we multiply both sides by a negative integer, the direction of inequality sign changes.

Thus, multiplying both sides by –6, we have:

 ⇨ z(–6) . (–6) ≥ 3 . (–6)

 ⇨ z ≥ –18

The graph of this solution set would be:

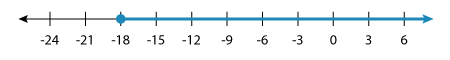
Note: The point –18 is plotted with a closed circle since the value (–18) is included in the solution set.

Solving Multi-Step Inequalities with Variables on Both Sides

What if both sides of inequality have the variable? Don’t be tripped up! It takes a few extra steps to isolate the variable on one side, but the procedure is the same. Here are some solved examples.

Example 1

Solve and graph 7(3x + 10) < 19x.

The graph of the solution set would be:

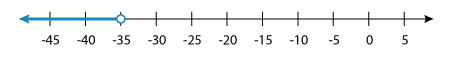
Example 2

Solve and graph 6x5 + 8 ≥ 10 + x.

Graphing the solution set, we have:

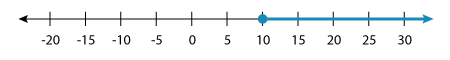
Example 3

Solve and graph 12x + 5 ≤ 1x – 11.

Graphing the solution set, we have:

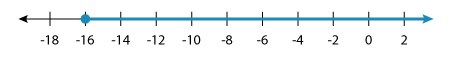
A Few Points to Ponder

• A multi-step inequality is an inequality whose solution set is obtained by performing multiple steps.

• To solve a multi-step inequality,

• ✯ simplify each side of the inequality,

• ✯ perform inverse operations, reverse the inequality symbol if the property suggests, and

• ✯ solve for the value of the variable.

• Plug a value from the solution set in the inequality to check if your solution set is right.

Boost your skills with our free printable Multi-Step Inequalities worksheets!