How to Solve One-Step Inequalities

Solving One-Step Inequalities: the Process in Brief

One-step inequalities are inequalities whose solutions are obtained by performing a single step. Follow this process to arrive at the solution:

  ✯ Bring the inverse operations into play.

  ✯ Isolate the variable on one side.

  ✯ Simplify the other side.

This might look exactly like solving one-step equations, but certain steps tend to change the direction of the inequality sign. So, be mindful of what affects the direction of the inequality symbol and what doesn’t.

What Doesn’t Change the Direction:

  1) Addition or subtraction of a number on both sides.

  2) Multiplication or division of a positive number on both sides.

Guessed what changes it? You’re right!

When you multiply or divide both sides by a negative number, you must reverse the direction of the inequality sign.

Now that you’ve understood the steps, let’s try implementing them to solve a variety of one-variable inequalities!

Solving One-Step Inequalities Using Addition

Addition is the inverse of subtraction. For inequalities of the form x – a < b, where ‘x’ is the variable, ‘a’ and ‘b’ are constants, we use the addition property of inequalities to solve. The property states that when you add the same number to both sides, the inequality remains unchanged.

We can understand this better by looking at a solved example.

Example

Solve the inequality: x – 2 < 3.

 ⇨ x – 2 + 2 < 3 + 2   [Adding 2 to both sides]

 ⇨ x < 5.

The solution set states that x can have any value that is less than 5.

A graphical representation of the solution set is as follows:

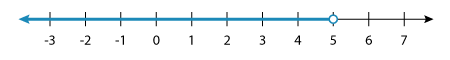
Note: Here, the value 5 is not included in the solution set, so it is plotted with an open circle.

Solving One-Step Inequalities Using Subtraction

We use the subtraction property to solve inequalities of the form x + a < b. The subtraction property states that the inequality remains unchanged when you subtract the same number from both sides.

Let’s take a look at a solved example:

Example

Solve this inequality: x + 3 ≥ 2.

 ⇨ x + 3 – 3 ≥ 2 – 3   [Subtracting 3 from both sides]

 ⇨ x ≥ –1.

When we graph this solution set, it looks like this:

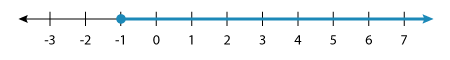
Note: Here, the value –1 is included in the solution set, so it is plotted with a closed or filled-in circle.

Solving One-Step Inequalities Using Multiplication

Multiplication is the inverse of division. Hence, when solving inequalities of the form xa < b, we apply the multiplication property. The variable has a fractional coefficient here. The property states that when we multiply the same number to both sides, the inequality remains the same.

Here, we have our solved example:

Example 1

Solve this inequality: x2 > –1.

 ⇨ x2 . 2 > (–1) . 2   [Multiplying 2 on both sides]

 ⇨ x > –2.

The graph of this solution set is:

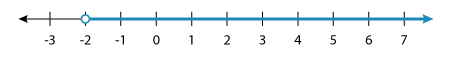
What if the variable has a negative fractional coefficient? Remember the change in the direction of inequality sign?

Yes, that happens when a negative number is multiplied. Here's a solved example to illustrate this.

Example 2

Solve the inequality: x–3 ≤ 2.

 ⇨ x–3 . (–3) ≥ 2 . (–3)   [Multiplying both sides by –3 and reversing the inequality symbol]

 ⇨ x ≥ –6.

Graphing this solution set, we have:

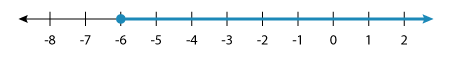
Solving One-Step Inequalities Using Division

For inequalities of the type ax < b, the division property is brought into play. It states that the inequality stays the same when we divide both of its sides by the same number. Isolate the variable by dividing both sides by the coefficient ‘a’. Always bear in mind that the sign reverses its direction when divided by a negative number.

Example 1

Solve the inequality: 4x ≥ 20.

 ⇨ 4x4 ≥ 204   [Dividing both sides by 4]

 ⇨ x ≥ 5.

When we graph this solution set, we get:

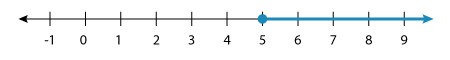
Example 2

Solve the inequality: –5x ≥ 10.

 ⇨ –5x–5 ≤ 10–5   [Dividing both sides by –5 and changing the direction of the inequality symbol]

 ⇨ x ≤ –2.

Graphing the solution set, we have:

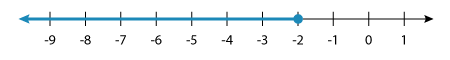
Wrapping Up!

• To solve inequalities with addition and subtraction, we need to isolate the variable on one side of the equation.

• To solve an inequality with the variable having a fractional coefficient, we use the multiplication property. We multiply both sides of the inequality by the denominator to isolate the variable.

• The division property is used to solve an inequality with the variable having an integer coefficient.

• Multiplication or division of a negative number on both sides of the inequality causes the inequality sign to change direction.

---