Prime Factorization | Methods and Examples

What Is Prime Factorization?

Prime factorization is the process of finding the prime numbers that can be multiplied to get the original number. It is a technique where we decompose a composite number and express it as a product of prime factors. Hence, it is sometimes referred to as prime factor decomposition.

Before we leap in, let’s refresh our knowledge of a few basics.

What Are the Factors of a Number?

Factors of a number are the numbers that you multiply to get that number.

Look at these examples:

2 = 1 x 2. Here, 1 and 2 are the two factors of 2.

3 = 1 x 3. The number 3 also has two factors: 1 and 3.

4 = 1 x 4. Also 4 = 2 x 2. So, the number 4 has three factors: 1, 2, and 4.

5 = 1 x 5. The number 5 has only two factors: 1 and 5.

6 = 1 x 6. Also 6 = 2 x 3, which means the number 6 has four factors: 1, 2, 3, and 6.

As you can see, some numbers have two factors, and some have more than two factors.

A number that has only two factors, 1 and the number itself, is called a prime number.

A number that has more than two factors is called a composite number.

Note: 1 = 1 x 1. So, 1 has only one factor. Thus, 1 is neither a prime nor a composite number.

Now that we know what prime numbers and factors are, let’s get cracking with finding the prime factorization of a number.

How Do You Find the Prime Factorization of a Number?

There are various techniques to find the prime factorization of a number. In this lesson we will demonstrate how to find it using the factor-tree method and the division method.

Prime Factorization Using Factor - Tree Method

The composite number that needs to be factored is the tree’s root. By resolving it into factors, the tree gets its branches. We first break the number down into a pair of factors and factorize any composite factor thus obtained.

Note: Use the Divisibility Rules to quickly determine the factors of a number.

Let’s find the prime factorization of 18 using a factor tree.

18 is an even number, which means it is divisible by 2.

18 = 2 x 9.

Let’s write that down on the branches of our factor tree.

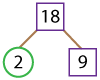
Here 2 is our first prime factor, so we have circled it. Now, we’ll need to find the factors of 9.

9 = 3 x 3.

With that, our factor tree gets two more branches.

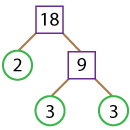
They can’t be factored any further! So, the number expressed as a product of prime factors is:

18 = 2 x 3 x 3.

Prime Factorization Using Division Method

Unlike the usual division operation that we perform, this method works upside down and involves successive division of the quotients by prime factors. The process goes on until a prime quotient is obtained.

Let’s find the prime factorization of 24 using the division method.

24 again is an even number, so it’s divisible by 2.

Now, let’s perform upside-down division with 2 as the divisor and 24 as the dividend.

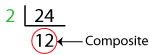
As 12 is composite, we need to repeat the process.

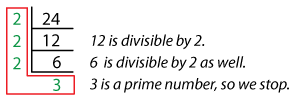
Now, the prime factorization of 24 is the product of all the prime numbers in the L-shape.

24 = 2 x 2 x 2 x 3.

To know how the factor-tree method works for the same problem, Click here!

We have the same prime factorization for 24, which is 2 x 2 x 2 x 3.

Order of the Factors Doesn’t Matter!

Every composite number has a unique prime factorization. So, you need not worry about the order in which you select the factor pairs. However you order them, you’ll have the same result.

Let’s now check if the statement is true with 45.

45 is an odd number, and it is not divisible by 2. So, we need to try the next number: 3.

The sum of the digits is: 4 + 5 = 9, which is divisible by 3. Hence, 45 is divisible by 3.

45 = 3 x 15.

Also, 45 has 5 as its last digit, which means it is divisible by 5 as well.

45 = 5 x 9.

Let’s draw factor trees for both these cases.

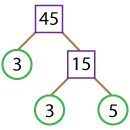
45= 3 x 3 x 5.

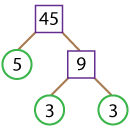
45= 5 x 3 x 3.

Now, let’s compare the two sets of factors obtained from both the cases.

The prime factorization of 45 is 3 x 3 x 5.

Note: The general rule is to write down the prime factors in ascending order.

Thus, no matter how you factor the number, you’ll end up with the same results.

Prime Factorization of a Number in Exponential Form

If prime factors are repeated, we can put them as powers. Exponential notation is an easy way of telling how many times a factor is repeated in a number.

Let’s take 64 for instance and factor it using the division method.

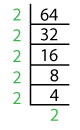
Now, expressing 64 as the product of prime factors we get:

64 = 2 x 2 x 2 x 2 x 2 x 2.

Here 2 is repeated 6 times, so the prime factorization in exponential form is:

64 = 2⁶.

It’s Your Turn Now!

Resolve 84 into prime factors and express the prime factorization in the exponential form.

The factor pairs could be

84 = 2 x 42.

84 = 3 x 28.

84 = 7 x 12.

No matter how you do it, you get the same answers.

Let’s start with the smallest prime number as usual.

The answer in exponential form is 84 = 2² x 3 x 7.

Hide answer

View answer

Looks like we have nailed prime factorization! This was easier than we anticipated, wasn’t it?

The Lesson in a Nutshell

• 1 is neither a prime nor a composite number.

• The factors of a number are the numbers that you multiply to get the number as the product. The factors of a number divide it out evenly.

• Every prime number has only two factors: 1 and the number itself.

• Composite numbers have more than two factors.

• The process of resolving a composite number into its prime factors is known as prime factorization.

• We can use either the factor-tree method or the division method to find the prime factorization of a number.

• In the factor-tree method, we start with a factor pair of the number, draw the factor tree, and continue to factor the number until a prime factor pair is obtained.

• In the division method, we divide the number using the prime factor, and perform successive division of every composite quotient obtained.

• The order in which you choose the factor(s) doesn’t really matter as every composite number has only one prime factorization.

• The prime factorization can be expressed in product form and exponential form.

Assess your skills with our free printable Prime Factorization worksheets.

---

Take a Prime Factorization Quiz Now!

Progress

Score

---

Continue

Restart Quiz

Sorry, your answer is incorrect.

Answer: