How to Simplify Fractions | Methods and Examples

Let's say you arrive at a fraction at the end of a calculation. We have been traditionally taught to reduce such a fraction to its lowest terms or rewrite it in the simplest form. Have you wondered why? Well in this lesson, we'll learn how to simplify fractions as well as know why we should simply fractions.

How to Reduce Fractions

Let's take a pizza, for instance, and slice it into six equal parts.

If you gobble 3 slices, what fraction of the pizza will be left over?

We'll have 36.

Now to make this fraction simpler, we can put the leftover pieces together.

You can see that one-half of the pizza is left. So, 36 when reduced or simplified is nothing but one-half.

Why Simplify Fractions

 ✯ Look at the pizza example above and find which is the easier way of talking about the part you ate: three-sixths of the pizza or half of the pizza. You will most likely root for "half", enabling us to unravel our first advantage – fractions in simplest form are easy to understand. This is why fractions abound in our day-to-day conversations, too.

 ✯ We use simplified fractions while measuring ingredients as in "a quarter tablespoon of sugar" or measuring water in the tank as in "three-fifths of the tank" for example.

 ✯ When we talk about partnerships, simplified fractions are a time-saver! We say for instance, "One-third of this property belongs to Fred, and the remaining two-thirds are owned by Nick."

 ✯ Finally, when we have complicated answers when solving mathematical problems, say, 78104, it's better if we reduce the answer to the lowest terms. Here, 78104 in its simplest form would be 34.

That's straightforward, isn't it?

Now, let's get back on track! Let's see how fraction simplification can be done mathematically.

Simplifying Fractions Using Prime Factorization

One simple, but very effective, way is to write the numerator and denominator as products of their prime factors.

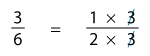
As you can see, the 3 in the numerator and the 3 in the denominator cancel out each other, and we are left with 12. Now we cannot reduce this any further as the only common factor between the numerator(1) and denominator(2) is 1.

As simple as ABC, isn't it?

Let's gallop through by reducing or simplifying one more fraction.

Example

Simplify 1215.

12 = 2 x 2 x 3

15 = 3 x 5

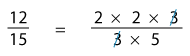
Multiplying what’s left, we have 45.

So, 1215 is reduced to 45.

Fraction Equivalence and Simplification

This is the method that brings equivalent fractions into play. Every step will require the application of divisibility rules, though. Let's, for example, rewrite 45108 in its lowest terms.

Both numbers are divisible by 3. So when we divide by 3, the equivalent fraction created thus would be:

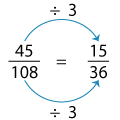
Again the numbers are divisible by 3. Repeating the step, we create another equivalent fraction.

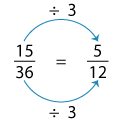
No factor is common now except 1; thus, 45108 in its simplest form is 512.

Reducing Fractions Using the GCF at One Stroke!

Rather than plowing through the multiple steps involved in canceling the common factors one after another, we can put any fraction in its simplest form at one stroke. Simply find the greatest common factor (GCF) of the numerator and denominator and cancel it out. This method works out faster when it comes to larger numbers.

Let's take the fraction 225240.

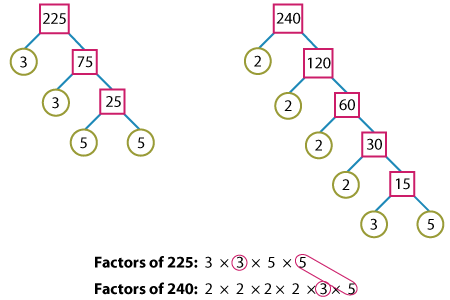
Therefore, GCF(225, 240) = 3 x 5 = 15.

Note: We can also find the prime factorization using the division method.

Now when we cancel off 15 from the fraction, we'll arrive at the simplest form of the fraction.

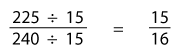
Thus, the simplest form of 225240 is 1516.

That was quick, wasn't it?

It's Your Turn Now!

1. Are these fractions in their simplest form?

a) 311  – Yes, it's in the simplest form.

b) 1327  – Yes, it's in the simplest form.

c) 1648  – No, it's not in the simplest form.

Hide answer

View answer

2. Simplify the following fractions.

a) 5566  5566 = 56

b) 13169  13169  = 113

c) 1640  1640 = 25

Hide answer

View answer

Wrapping-Up!

• A fraction is easier to interpret in its simplest form.

• A fraction can't be reduced further if its parts have only '1' as the common factor.

• We can simplify a fraction by using the prime factorization of the numerator and denominator, by canceling out the greatest common factor from them, or by creating an equivalent fraction.

---