How to Solve Systems of Equations Using Cramer’s Rule

As well as refreshing readers’ memory of the basic methods of solving a system of equations, this lesson educates them on a more advanced strategy that involves matrices and determinants. Named after its author Gabriel Cramer, this technique is popularly known as Cramer’s Rule.

What is Cramer’s Rule?

Let’s suppose we have a system of equations with two variables

ax + by = e

cx + dy = f

We can rewrite this system in the matrix notation as:

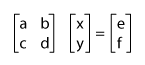
where

Cramer’s rule states that:

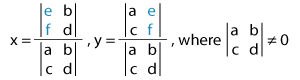
Note: We need to replace the first column of the coefficient determinant with the elements of the constant matrix to solve for x and replace the second column with it to solve for y.

Similarly, for a system of equations with three variables,

ax + by + cz= j

dx + ey + fz = k

gx + hy + iz = l

Cramer’s rule states that:

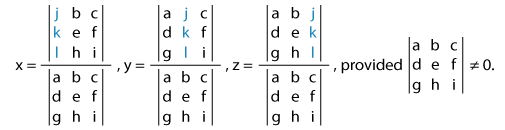
Note: We need to replace the first, second, and third columns of the coefficient determinant with the elements of the constant matrix to solve for x, y, and z respectively.

Solving Systems of Equations with Two Variables Using Cramer’s Rule

Let’s solve this 2-variable linear system using Cramer’s rule.

3x + y = 1

x – 2y = 5

First, we need to evaluate the determinant of the coefficient matrix.

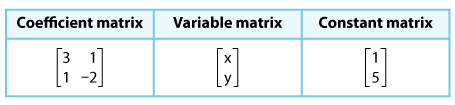
The determinant of the coefficient matrix is:

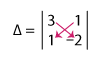
   = 3(–2) – 1(1)

   = –6 – 1

 Δ = –7

We have a nonzero coefficient determinant. Let’s proceed to our next step: solving for x.

Note: When Δ = 0, the system either has no solution or infinitely many solutions. Cramer's rule cannot be applied in this case.

When we replace the x-column of the coefficient determinant with the constant matrix, we have:

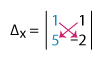
   = 1(–2) – 1(5)

   = –2 – 5

 Δx = –7

When we replace the y-column of the coefficient determinant with the constant matrix, we have:

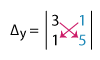
   = 3(5) – 1(1)

   = 15 – 1

 Δy = 14

Now, we are all set to apply the Cramer’s rule. As per the rule, we have:

   x = ΔxΔ , y = ΔyΔ

Plugging in the appropriate values, we have:

  x = –7–7, y = 14–7

 ⇨ x = 1, y = –2

Thus, the solution of our system is (1, –2).

Now that we have understood the steps, let’s implement the rule to a system of equations with 3 variables.

Solving Systems of Equations with Three Variables Using Cramer’s Rule

Cramer’s Rule is the most efficient method for solving systems of 3 or more equations, as all other methods involve a series of steps. The major advantage is that we can choose to solve for any one variable and don’t need to solve the whole system.

Let’s solve this system using Cramer’s rule.

x + y + 2z = 6

2x + y + 3z = 10

x + 2y – z = –20

To solve this system using Cramer’s Rule, the determinant of the coefficient matrix should be a nonzero number. Let’s illustrate this.

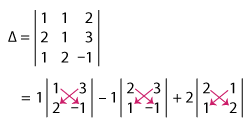
  = 1(–1 – 6) – 1(–2 – 3) + 2(4 – 1)

  = 1(–7) – 1(–5) + 2(3)

  = –7 + 5 + 6

 Δ = 4

Δ ≠ 0; so let’s press on with finding Δx, Δy, and Δz.

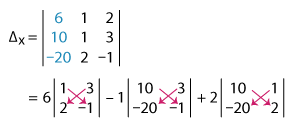
   = 6(–1 – 6) – 1(–10 + 60) + 2(20 + 20)

   = 6(–7) – 1(50) + 2(40)

   = –42 – 50 + 80

 Δx = –12

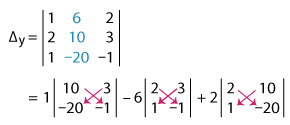
   = 1(–10 + 60) – 6(–2 – 3) + 2(–40 – 10)

   = 1(50) – 6(–5) + 2(–50)

   = 50 + 30 – 100

 Δy = –20

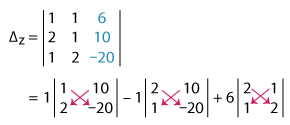
   = 1(–20 – 20) – 1(–40 – 10) + 6(4 – 1)

   = 1(–40) – 1(–50) + 6(3)

   = –40 + 50 + 18

 Δz = 28

Now, let’s apply the Cramer’ rule.

 x = ΔxΔ, y = ΔyΔ , z = ΔzΔ

Substituting the relevant values, we have:

 x = –124, y = –204, z = 284

 x = –3, y = –5, z = 7

Thus, the solution of our system is (–3, –5, 7).

Example

Solve for z using Cramer’s rule.

 –y + z = –3 – 7x

 5y – z = 26 – 2x

 y – 2z = –24 – 8x

Rearranging the equations in standard form:

 7x – y + z = –3

 2x + 5y – z = 26

 8x + y – 2z = –24

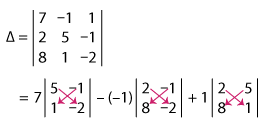
  = 7(–10 + 1) + 1(–4 + 8) + 1(2 – 40)

  = 7(–9) + 1(4) + 1(–38)

  = –63 + 4 – 38

 Δ = –97

Solving for z using Cramer’s rule:

 z = ΔzΔ

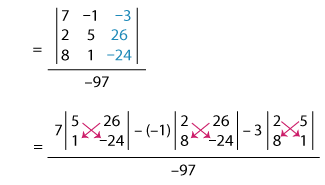
   = 7(–120 – 26) + 1(–48 – 208) – 3(2 – 40)–97

   = 7(–146) + 1(–256) – 3(–38)–97

   = –1,022 – 256 + 114–97

   = –1,164–97

   z = 12

Thus, the value of the variable z is 12.

Evaluate 3x3 Determinants Instantly Using Determinant Calculator!

A Quick Recap!

• Cramer’s rule is effective when solving systems of equations with 3 or more variables.

• Cramer’s Rule helps us solve for any specific variable, and we don’t need to solve the whole system each time.

• We can apply the Cramer’s rule only when Δ≠0.

• When Δ = 0, the system either has no solution or has infinitely many solutions.

---