How to Solve Two-Step Inequalities
- Math Lessons >
- Two-Step Inequalities
You have seen how to solve one-step inequalities. It’s now time to step up your game with two-step inequalities!
Solving Two-Step Inequalities – One Step at a Time!
Two-step inequalities are the inequalities consisting of one variable and any two operations. They also require exactly two steps to obtain the solution.
The objective of solving two-step inequalities is to isolate the variable. For that, you must perform the following operations:
Step 1: Add or subtract the constants on both sides of the inequality.
Step 2: Multiply or divide both sides of the inequality by the coefficients of the variable.
Keep simplifying both sides of the inequality until only the variable is left on one side.
Solving Two-Step Inequalities with Inverse Operations
To solve two-step inequalities, identify which two operations are involved and use their inverse.
Let's take the inequality 3x + 5 < 11 for instance.
This inequality involves addition and multiplication, so the inverse operations to use are subtraction and division.
First,we need to isolate the term 3x. By subtracting 5 on both sides, we get:
3x + 5 – 5 < 11 – 5
3x < 6
To isolate x, we must divide both sides by 3. This way, we will be left with only x on one side.
3x3 < 63
⇨ x < 2
When we graph this inequality, we get:
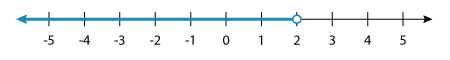
Note: An open circle is used to mark the value 2 because the value is not included in the solution set.
Thus, performing the inverse operations is essential to obtaining the solution set.
Taking a look at a few examples will help us get more insight.
Example 1
Solve and graph the inequality: –2z – 4 ≥ 6.
Since this inequality involves subtraction and multiplication, we should perform the inverse operations: addition and division respectively.
–2z – 4 + 4 ≥ 6 + 4
[Adding 4 on both sides]
–2z ≥ 10
[Simplifying]
–2z–2 ≤ 10–2
[Dividing by – 2 and flipping the sign]
⇨ z ≤ –5
When we graph this solution on a set number line, we get:

Note: Notice how a closed circle is used to mark – 5? This is because the value is included in the solution set.
Check Your Solution!
Replace the variable in the inequality with a value from the solution set to double-check your answer.
Let us take z = –8
–2z – 4 ≥ 6
–2(–8) – 4 ≥ 6
16 – 4 ≥ 6
12 ≥ 6 ✔
Example 2
Solve and graph the inequality x – 2–4 < –2.
This inequality involves division and subtraction.
To isolate x, we must multiply both sides by –4.
Remember when multiplying or dividing by a negative number, we need to flip the inequality sign.
x – 2–4 < –2
[The given inequality]
(–4) . x – 2–4 > (–4)(–2)
[Multiplying both sides by – 4, flipping the sign]
x – 2 > 8
[Simplifying]
x – 2 + 2 > 8 + 2
[Adding 2 on both sides]
⇨ x > 10
A graphical representation of the solution set would be:
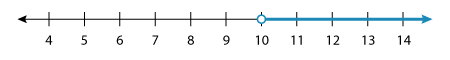
Solving Two-Step Inequalities When a Variable Appears Twice
Sometimes, the variable may appear on both sides of a two-step inequality. To solve such inequalities, we need to find the term that can be easily removed and perform the inverse operation so only one term containing the variable is left.
Example
Solve and graph the inequality 2x > 65 – x.
2x > 65 – x
[The given inequality]
2x + x > 65 – x + x
[Adding x on both sides]
3x > 65
[Simplifying]
3x3 > 65 .13
[Dividing by 3 on both sides]
⇨ x > 25
[Simplifying]
Notice that solving this inequality requires two steps – first, by using addition and second, by using division on both sides. The trick is to remove the terms one by one until we are left with the solution set for the inequality on one side.
Two-Step Inequalities in the Real World
In the real world, people like managers, analysts, engineers, programmers, builders, and even health-care professionals heavily draw on inequalities. The odds are that you’ve formed and solved inequalities in your life without even knowing it yourself!
The following example shows us how easy it is to use two-step inequalities to find solutions to real-life problems.
The cost of one paint can is $12 and the cost of one paint brush is $7. Mark has $79. How many cans can he buy and still afford to buy a brush?
Since we need to find the number of cans, let the number be x.
As the price of one can is $12, he can spend 12x dollars.
He must also purchase a $7 brush, which makes it 12x + 7.
Since he has $79, the total cost of the items must be less than or equal to 79.
With all this information, we obtain the inequality:
12x + 7 ≤ 79
12x + 7 – 7 ≤ 79 – 7
[Subtracting 7 on both sides]
12x ≤ 72
[Simplifying]
12x12 ≤ 7212
[Dividing both sides by 12]
⇨ x ≤ 6
Therefore, Mark can buy up to six cans of paint along with one brush.
A Quick Review
To solve two-step inequalities, isolate the variable on one side. This is done using the inverse operations of addition or subtraction and multiplication or division.
When multiplying or dividing on both sides of the inequality by a negative number, the inequality sign will change direction.
It’s always a good idea to plug a value from the solution set in the inequality to check if the solution is right.

Strengthen your learning parameters with our free printable Two-Step Inequalities worksheets.

