How to Find the Volume of Cylinders

Look at these cylinder-shaped objects.

What is the capacity of the can?

What is the amount of wax used to make the candle?

How much perfume can the bottle hold?

How much water can the tank hold?

You would be able to answer these questions only if you know how to calculate the volume of cylinders.

The volume of a cylinder is the measure of how much three-dimensional space a cylinder takes up.

In this lesson, we are going to learn to find the volume of cylinders.

Volume of a Cylinder - Formulas and Real-Life Examples

The volume(V) of a cylinder is the product of the area of its base(B) and its height(h). Let’s write it as a formula.

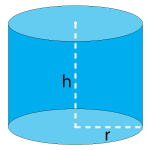
Here, “r” is the radius of the circular base and “h” is the height of the cylinder.

Now that we know the formula, all we need to do is plug in the dimensions and calculate the volume of cylinders. You can also find a missing height or radius of the cylinder by rearranging the formula. Let’s take a look at some examples.

Example 1

How much water can this cylindrical aquarium hold? (Use π ≈ 3.14)

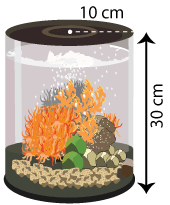
Given that, r = 10 cm and h = 30 cm.

Now, let's apply the formula.

Volume of the cylinder = πr²h

V = π (10 cm)² (30 cm)   [Substituting r and h]

V = π (100 cm²) (30 cm)   [Squaring 10 cm]

V = π (3,000 cm³)

V ≈ 3.14 (3,000 cm³)   [Using π ≈ 3.14]

V ≈ 9,420 cm³

Thus, the aquarium can hold approximately 9,420 cm³ of water.

Example 2

Find the volume of the coffee mug. Round your answer to two decimal places. (Use π ≈ 3.14)

The dimensions of the coffee mug are r = 1.5 in and h = 4.4 in.

We know that volume of the cylinder = πr²h

V = π (1.5 in)² (4.4 in)   [Substituting r and h]

V = π (2.25 in²) (4.4 in)   [Squaring 1.5 in]

V = π (9.9 in³)

V ≈ 3.14 (9.9 in³)   [Using π ≈ 3.14]

V ≈ 31.09 in³   [Rounding off to two decimal places]

The volume of the cylindrical mug is approximately 31.09 cubic inches.

Example 3

What is the volume, in gallons, of this cylindrical paint can? Use π ≈ 3.14 and round your answer to two decimal places. (Hint: 1 gal = 231 in³)

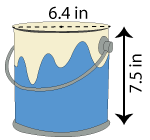
We are given the paint can's diameter this time, d = 6.4 in.

We know that radius = diameter2. Let's plug-in the diameter here. We would have:

Radius of the paint can = 6.4 in2

 ⇨ r = 3.2 in

Now, the volume of the cylinder is: V = πr²h

V = π (3.2 in)²(7.5 in)   [Substituting r and h]

V = π (10.24 in²)(7.5 in)   [Squaring 3.2 in]

V = π (76.8 in³)

V ≈ 3.14 (76.8 in³)   [Using π ≈ 3.14]

V ≈ 241.15 in³   [Rounding off to the nearest hundredth]

Now, let's use our hint, 1 gal = 231 in³ and figure out the volume in gallons.

To obtain the volume in gallons, we need to use the conversion factor 1 gal231 in³.

 ⇨ V ≈ 241.15 in³ × 1 gal231 in³

 ⇨ V ≈ 1.04 gal   [Simplifying and rounding off to two decimal places]

∴ The volume of the paint can is approximately 1.04 gallons.

How to Find the Missing Parameters of a Cylinder Using Volume

Now that we have mastered calculating the volume of cylinders, let's press on and determine the missing parameters of a cylinder using its volume. We can find a missing radius or height of a cylinder if we know its volume. All we need to do is rearrange the formula with the missing dimension as the subject. Let's do that for the height and radius now.

Recalling our formula, we have V = πr²h.

Isolating the height of the cylinder on one side, we have:

h = Vπr²

Isolating the radius of the cylinder on one side, we have:

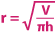
Let's take a look at some examples with missing measures now!

Example 1

A cylindrical candle has 452.16 cubic centimeters of wax. If the diameter of its base is 6 centimeters, what is the height of the candle? (Use π ≈ 3.14)

The volume of wax the candle is made of is V = 452.16 cm³. Its base diameter is d = 6 cm.

We know that r = d2

 ⇨ r = 6 cm2

 ⇨ r = 3 cm

Let’s now substitute the radius and volume in the formula h = Vπr², we get:

h = 452.16 cm³π (3 cm)²

h = 452.16 cm³π (9 cm²)   [Squaring 3 cm]

h ≈ 452.16 cm³3.14 (9 cm²)   [Using π ≈ 3.14]

h ≈ 452.16 cm³28.26 cm²

h ≈ 16 cm

The height of the candle is approximately 16 cm.

Example 2

A cylindrical soup can has a capacity of 34.55 cubic inches and height of 3.8 inches. Find the radius of its base. Round your answer to nearest tenth. (Use π ≈ 3.14)

We are given the volume and height of the soup can, V = 34.55 in³ and h = 3.8 in.

So, the radius of the soup can is approximately 1.7 inches.

Wrapping Up!

• The volume of a cylinder is the measure of how much three-dimensional space a cylinder takes up.

• The area of the circular base times the height of the cylinder will give you the volume of the cylinder.

• The formula for calculating the volume of cylinders is V = πr²h, where r is the base radius and h is the height of the cylinder.

• To find a missing radius or height of the cylinder, we need to rearrange the formula with the unknown measure as the subject.

---