How to Solve One-Step Equations

What Are One-Step Equations?

One-step equation, as the name suggests, is solved in a single step using just one operation. To solve one-step equation, we need to isolate the variable and obtain its value.

In this lesson, we’ll learn how to solve one-step equations that involve each of the four operations.

How to Solve One-Step Equations Involving Addition

Look at the equation.

x + 3 = 12

To solve this equation, all we need to do is find a value of the variable x that will make the equation true.

But, what should we add to 3 to make it equal to 12?

Our first goal is to rearrange the equation with the variable x left by itself on one side. This isolation is done by using inverse operations. Here, the inverse of addition is subtraction.

To get rid of the +3, we’ll need to subtract 3.

We can’t simply do that on one side. We’ll have to strike a balance between the two sides of the equation,so whatever is done on one side should be done on the other side too.

Understand the balance between both sides of the equation with a click on the balance!

So let’s subtract 3 from both sides.

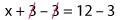
Both +3 and –3, the zero pair, cancel out each other and leave us with x on one side and 9 on the other side.

⇨ x = 9

Thus, the value of x is 9.

Example

Solve for z if z + 9 = 15.

  z + 9 = 15   [Given equation]

  z + 9 – 9 = 15 – 9   [Subtracting 9 from both sides]

 ⇨ z = 6   [Simplifying]

How to Solve One-Step Equations Involving Subtraction

Now, let’s move on to the next equation that involves subtraction.

y – 8 = 7

The inverse of subtraction is addition. So, our first step is to make the variable stand alone on one side by adding 8 on both sides, maintaining the balance.

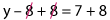
Now the –8 and +8 cancel out, and we have our variable y all by itself. Adding the numbers on the other side we have:

y = 15

Thus, the value of y is 15.

Example

Solve for h if h – 2 = –14.

  h – 2 = –14   [Given equation]

  h – 2 + 2 = –14 + 2   [Adding 2 to both sides]

 ⇨ h = –12   [Simplifying]

How to Solve One-Step Equations Involving Multiplication

Let’s take an equation that involves multiplication.

6p = 48

To solve this equation, we’ll have to isolate the variable p and get rid of its coefficient, which is 6 in this case.

Which operation should we use here? Yes, the opposite operation of multiplication is division.

But we need to divide not just one but both the sides of the equation by 6 to keep it well-balanced.

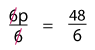
Dividing 48 by 6, we’ll have:

p = 8

Thus, the value of p is 8.

Example

Solve –5q = 35.

  –5q = 35   [Given equation]

 –5q–5 = 35–5   [Dividing both sides by –5]

 ⇨ q = –7   [Simplifying]

How to Solve One-Step Equations Involving Division

Let’s move on to the next equation with division.

m5 = 12

Our first step is to isolate the variable m as usual. The inverse of division is multiplication. Now to undo division by 5, we need to multiply by 5. We’ll do that on both sides of the equation to maintain the balance.

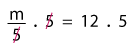
The 5s on the left side cancel each other. Multiplying the numbers on the right, side we have:

m = 60

We have solved our equation.

Example

Solve k4.2 = 16.5.

  k4.2 = 16.5  [Given equation]

 k4.2 . (4.2) = 16.5 . (4.2)   [Multiplying both sides by 4.2]

 ⇨ k = 69.3   [Simplifying]

A Quick Recap!

• To solve a one-step equation,

•  ✯ Identify the variable whose value you need to find.

•  ✯ Figure out the opposite operations.

•  ✯ Ensure the equality or balance is maintained.

•  ✯ Solve and find the value of the variable.

• If you want to make sure your answer is right, then plug the value back into the original equation, and if that makes the equation true, your answer is right.

---