How to Find the LCM | Methods and Examples
- Math Lessons >
- LCM
Overview of Least Common Multiple:
- What is LCM?
- Least Common Multiple - Video Lesson
- How Do You Find the LCM by Listing the Multiples?
- How Do You Find the LCM Using Prime Factorization?
- What Actually Happens in Step 2?
- How Do You Find the LCM Using Repeated Division?
- LCM of More Than Two Numbers
- LCM in Our Everyday Life
- Calculate the LCM of up to Three Numbers Instantly Using LCM Calculator!
- The Lesson in a Nutshell
- Least Common Multiple - Quiz
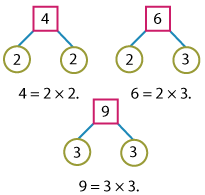
What is LCM?
The least common multiple, abbreviated as LCM, is the smallest number that is a multiple of two or more numbers. There are various ways to find the least common multiple of a set of numbers. In this lesson, we are going to talk you through three ways, rather three effective techniques, of finding the LCM. Let's learn them one by one.
How Do You Find the LCM by Listing the Multiples?
To determine the LCM of smaller numbers, we use listing-the-multiples method. This is a simple method where we compare the multiples of the numbers, pick out the matching multiples, and choose the lowest of those.
Let’s get started with a pair of numbers: 2 and 3. Let’s draw a number line to quickly identify the multiples.

Here, the multiples of 2 are 2, 4, 6, 8, 10, 12, and so on; the multiples of 3 are 3, 6, 9, 12, and so on.
Now, let’s compare the multiples of 2 with those of 3 and pick the common ones.
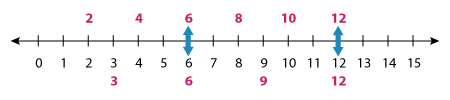
As you can see, the common multiples are 6, 12, and so on. But, we need to look for the least common multiple!
Thus, we have LCM (2, 3) = 6.
Fast Fact 1
The least common of multiple of two prime numbers is simply their product.
In the above example, 2 and 3 are prime numbers.
⇨ The LCM of 2 and 3 is nothing but 2 x 3 = 6.
Example 1
Determine the LCM of the number pair 6 and 8.
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48,...
Multiples of 8: 8, 16, 24,...
Note: As soon as you’ve found the first common multiple, you can stop listing the multiples. Hence, we have stopped with 24 here.
Thus, 24 is the least common multiple of 6 and 8.
Example 2
What is the LCM of 11 and 13?
Here, 11 and 13 are prime numbers.
Therefore, the LCM of 11 and 13 is 11 x 13 = 143.
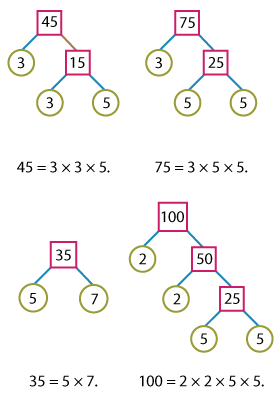
How Do You Find the LCM Using Prime Factorization?
When we need to calculate the LCM of larger numbers, where listing the multiples is probably not the best idea as it requires a longer list, we use prime factorization. Here’s how it works step by step:
Step 1: Express each number as the product of prime factors.
Step 2: Write down each factor the greatest number of times it occurs in a number.
Step 3: Multiply the factors to figure out the least common multiple.
Let’s find the LCM of two numbers using prime factorization.
First, we need to decompose 56 and 78 into prime factors using factor trees.

Generate factor trees for 56 and 78 with a click on the number!
Now, expressing both the numbers as the product of prime factors, we have:
56 = 2 x 2 x 2 x 7.
78 = 2 x 3 x 13.
That is the end of step 1. Now, let’s move on to step 2: identifying how many times a factor occurs.
Here, 2 occurs a maximum of 3 times in a number; 3, 7, and 13 appear once.
Now, our final step is the product of the factors: 2 x 2 x 2 x 3 x 7 x 13.
∴ LCM (56, 78) = 2,184.
What Actually Happens in Step 2?
Why do we select each factor the greatest number of times it appears in a number? To understand this better, let’s use a Venn diagram. Let’s represent the factors on the diagram.
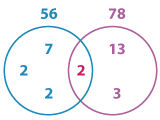
The diagram shows the common factor 2 placed on the intersection of the two circles and the other factors in the respective circles.
Now, the LCM is the product of the prime factors on the overlapping and non-overlapping parts.
That clarifies why a factor is written the greatest number of times it occurs in a number.
The LCM (56, 78) is 2 x 2 x 2 x 3 x 7 x 13 = 2,184.
Example 1
Determine the LCM of 52 and 22 using prime factorization.
Resolving 52 and 22 into factors, we have:
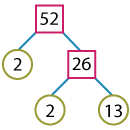
52 = 2 x 2 x 13.
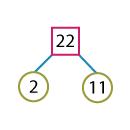
22 = 2 x 11.
The product of the factors is 2 x 2 x 13 x 11. Thus, the LCM (52, 22) = 572.
Example 2
Use prime factorization to find the LCM of 18 and 46.
The factor trees for 18 and 46 are shown below.
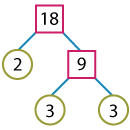
18 = 2 x 3 x 3.
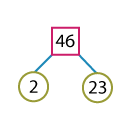
46 = 2 x 23.
The product of the factors is 2 x 3 x 3 x 23. Thus, the LCM (18, 46) = 414.
How Do You Find the LCM Using Repeated Division?
Repeated division, also called successive division or the ladder method, is a fast-track method of calculating the LCM of a pair of numbers. All you need to do is divide both the numbers simultaneously by a common prime factor. Continue to divide them until you have no factors in common.
Let’s now find the LCM of 60 and 84.

Click on the number to view the repeated division of 60 and 84!
Now the least common multiple is the product of the common prime factors and the resultant quotients. That is to say, we need to multiply all the factors outside the ladder in the L-shape.
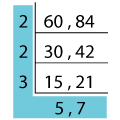
Thus, the LCM (60, 84) is 2 x 2 x 3 x 5 x 7 = 420.
Example 1
Calculate the LCM of 36 and 108 using the ladder method.
Implementing the ladder method 36 and 108, we have

The product of the factors is 2 x 2 x 3 x 3 x 3. Thus, the LCM (36, 108) = 108.
Example 2
Find the LCM of 49 and 63 using successive division.
Dividing 49 and 63 simultaneously and successively by common factors, we have
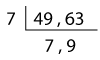
The product of the factors is 7 x 7 x 9 = 441. Thus, the LCM (49, 63) = 441.
If the numbers don’t have a common factor, the LCM is their product.
For instance, when we resolve 25 and 12 into their factors, we have,
25 = 5 x 5.
12 = 2 x 2 x 3.
Neither of the two numbers has any factors in common.
Thus, their LCM is 25 x 12 = 300.
Fast Fact 3
If one number is the factor of the other, their LCM is the greater number.
Let’s suppose we are finding the LCM of 9 and 45. Let’s break it down into prime factors.
9 = 3 x 3.
45 = 3 x 3 x 5.
Now, the common factors are two 3s and the non-common factor is 5. Their Product is 3 x 3 x 5 = 45.
Thus, the LCM (9, 45) = 45.
If you observe the numbers carefully, you’ll find that 9 is a factor of 45. Hence, without going step by step as shown above, you can directly conclude that the greater number 45 is the LCM.
LCM of More Than Two Numbers
Let’s take our learning to the next level and practice finding the LCM of three numbers. Take 3, 6, and 9 for instance.
We’ll find the LCM using all the three methods we’ve learnt so far.
Lists of Multiples
Multiples of 4:
4, 8, 12, 16, 20, 24, 28, 32, 36,...
Multiples of 6:
6, 12, 18, 24, 30, 36,...
Multiples of 9:
9, 18, 27, 36,...
Thus, the LCM(4, 6, 9) = 36.
Prime Factorization
Product of the factors:
2 x 2 x 3 x 3.
Thus, the LCM(4, 6, 9) = 36.
Ladder Method
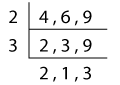
Product of the factors:
2 x 2 x 3 x 3.
Thus, the LCM(4, 6, 9) = 36.
Let’s learn how to find the LCM of 4 numbers: 45, 72, 85, and 100 this time.
We are up against comparatively larger numbers, so let’s work it out using prime factorization and the ladder method.
Prime Factorization
Product of the factors: 2 x 2 x 3 x 3 x 5 x 5 x 7.
LCM (45, 75, 85, 100) = 6,300.
Ladder Method

Product of the factors: 5 x 3 x 5 x 3 x 7 x 4.
LCM (45, 75, 85, 100) = 6,300.
No matter how many numbers you have, you can find their LCM using any of these three methods.
LCM in Our Everyday Life
Wondering if LCM has anything to do with our everyday life? There are innumerable instances where we use LCM every day. Let’s discuss one of those scenarios here:
Susan and Amanda take guitar lessons at the School of Music in Brooklyn. Susan takes guitar lessons every 4 days, and Amanda takes them every 5 days. If they both took guitar lessons today, how many days will it be until they take the guitar lessons on the same day again?

This scenario can be easily solved by listing the multiples. Let’s work it out quickly.
Susan’s guitar lessons are scheduled every 4 days. So, Susan’s schedule is nothing but the multiples of 4:
4, 8, 12, 16, 20, 24, and so on.
Amanda takes the guitar lessons every 5 days. So, Amanda’s guitar lessons are scheduled as the multiples of 5:
5, 10, 15, 20, 25, 30, and so on.
When we compare both lists, we can find that 20 is the least common multiple.
Therefore, Susan and Amanda will take their guitar lessons on the same day again after 20 days.
Tip: Instead of listing the multiples, this can be solved with this simple fact. 4 and 5 have no factors in common, so their LCM is 4 x 5 = 20.
Calculate the LCM of up to Three Numbers Instantly Using LCM Calculator!
Type the numbers in the text boxes, and calculate their LCM with a click of your mouse!
The Lesson in a Nutshell
The LCM of a set of numbers is the smallest number that is divisible by every number in the set.
We can find the LCM of a set of numbers by listing the multiples, by using prime factorization, or by performing repetitive division.
To find the LCM by listing the Multiples,
✯ List the multiples of each number.
✯ Figure out the common multiple.
✯ Select the least.
✯ Extend the list until you find a multiple in common.
Prime factorization is a technique wherein a composite number is broken down into its prime factors. To find the LCM,
✯ Express each number as a product of prime factors.
✯ Write down each factor the greatest number of times it occurs in a number.
✯ Determine the product of the factors.
To find the LCM using the ladder method,
✯ Use the divisibility rules and divide the numbers simultaneously by a common factor.
✯ Continue to divide until you end up with prime quotients or those that have no factors in common.
✯ Multiply the factors outside the ladder in the L-shape.

Test your skills with our free printable Least Common Multiple worksheets!

