Prime and Composite Numbers | Definition, Facts, and Examples

In this lesson, we'll take a look at what prime numbers and composite numbers are and will explain how to identify them. Let’s first figure out what prime numbers and composite numbers mean.

What Are Prime and Composite Numbers?

A composite number is a number that can be divided by a whole number other than 1 and itself. A prime number, on the other hand, can’t be divided by any number other than 1 and itself.

Identifying If a Number Is Prime or Composite by Sharing

Imagine you have 6 donuts. How many different ways can you share them in?

We can make 2 groups with 3 donuts in each,

Or 3 groups of 2 donuts in each,

Or 6 groups with 1 donut in each.

How would you share 9 donuts?

We can, obviously, group them into 9 groups of 1 each. And also divide the donuts evenly in groups of 3 donuts each.

How would you share if there were 7 donuts?

The only way of sharing the 7 donuts would be by putting them into 7 groups of 1 each.

We can’t divide the 7 donuts into equal groups without having any left over.

The numbers 6 and 9 can be divided by other whole numbers, such as 2 and 3; but 7 can be divided by only 1 or itself.

So we understand that 6 and 9 are composite numbers, and 7 is a prime number.

Identifying If a Number Is Prime or Composite Using Its Factors

Another method of quickly checking whether a number is prime or composite is by using its factors. If you’re wondering what factors are, they are the numbers that you multiply to get another number.

Let’s take a look at the first few prime numbers.

1 = 1 x 1. 1 is the only factor of 1. So, it is neither prime nor composite.

2 = 1 x 2. 2 has exactly 2 factors: 1 and 2. So, it is a prime number.

3 = 1 x 3. 3 also has exactly 2 factors: 1 and 3. So, it is a prime number.

4 = 1 x 4; 4 = 2 x 2. 4 has 3 factors: 1, 2, and 4. So, 4 is a composite number.

5 = 1 x 5. 5 has just 2 factors: 1 and 5. So, 5 is a prime number.

6 = 1 x 6; 6 = 2 x 3. Thus, 6 has 4 factors: 1, 2, 3, and 6. So, 6 is a composite number.

So with small numbers, your job of telling whether a number is prime or composite is super-easy. The quickest way of finding the factors of larger numbers, though, is by using the divisibility rules.

Here are a few examples.

Example 1

Is the number 267 prime or composite?

Listing the factors of this number would be time-consuming. So, we’ll bring the divisibility rules into play.

267 is not an even number, so it’s not divisible by 2.

Now, the divisibility test for 3 is to check if the sum of the digits is divisible by 3.

The sum of the digits of 267 is:

2 + 6 + 7 = 15

Now, 15(= 3 x 5) is a multiple of 3. So, 267 is divisible by 3.

Thus, 267 is composite.

Example 2

Is 37 a prime or composite number?

Let’s perform the divisibility tests one by one.

37 is not an even number, so it’s not divisible by 2. Subsequently, 37 is not divisible by 4, 6, or 8.

Next, the sum of the digits of 37 is: 3 + 7 = 10. 10 is not divisible by 3. So, 37 is not divisible by 3.

Now, the last digit of 37 is neither 0 nor 5, so it’s not divisible by 5 as well.

As 37 cannot have any factor greater than 6, we can stop with 6.

Thus, 37 is a prime number.

Finding Prime Numbers Using Sieve of Eratosthenes

An interesting way of finding prime numbers is by using the Sieve of Eratosthenes. This method works on the idea of sifting the composite numbers to identify the prime numbers. Let's pass the numbers up to 50 through the sieve now!

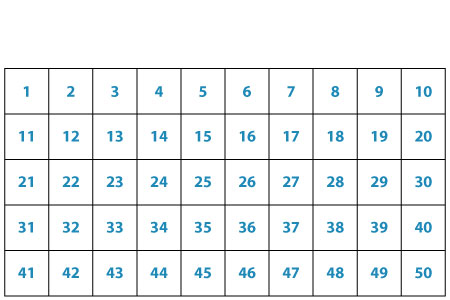
Filter out the composite numbers with a click on the chart!

Go ahead and extend this method to any number and scout out the prime and composite numbers in no time!

Lists of Prime and Composite Numbers from 1 to 100

It’s Your Turn Now!

Intriguing Facts about Primes!

• ✯ The largest prime number found so far has 24,862,048 digits!

• ✯ Thanks to Euclid, who was instrumental in theorizing the idea, every composite number can be written as a product of prime numbers. Check it out for yourself!

• ✯ There’s an organization dedicated to research on prime numbers - Great Internet Mersenne Prime Search (GIMPS).

A Quick Recap

• A prime number has exactly two factors: 1 and the number itself.

• Composite numbers have more than two factors.

• The numbers 0 and 1 are neither prime nor composite.

• Prime numbers are also called non-composite numbers.

• We can identify whether a number is prime and composite by checking if the number can be shared into equal groups, or listing all its factors, or applying the divisibility rules, or using the sieve of Eratosthenes.

---