Slope | Definition, Formulas, Types, and Examples

What Is a Slope?

Have you ever ridden a bike uphill or skied downhill? Then you sure know what a slope is. Look at these pictures.

All these are examples of slopes. Mathematically speaking, a slope, or gradient, is a number that describes the steepness of a line.

In this lesson, we’ll learn what a slope is and how to find the measure of a slope on a Cartesian plane. We’ll also identify the different types of slopes.

How to Find the Slope of a Line

Here we have a straight line on a coordinate plane.

What do you think is its steepness? Do we have any formula to calculate it? Of course it’s a yes!

The slope or gradient of a line is the ratio of the vertical distance (rise) to the horizontal distance (run) between any two points on a line. It is denoted by the letter “m”.

Let’s understand the formula! Our first step is to plot two points, namely (x₁, y₁) and (x₂, y₂), on the line.

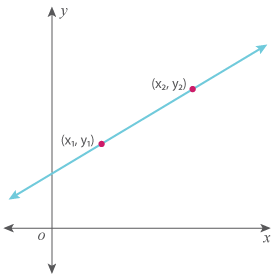
Now, let’s run horizontally from (x₁, y₁) and stop at a point from where we can rise vertically to reach (x₂, y₂). We would have a right triangle by this step.

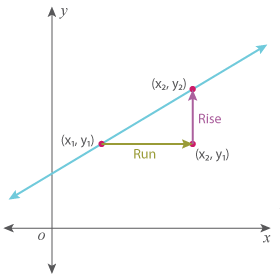
Let’s contemplate on the rise and run now. We have moved horizontally from x₁ to x₂, and then vertically from y₁ to y₂. So, simply put, run is the change in x (∆x) and rise is the change in y (∆y).

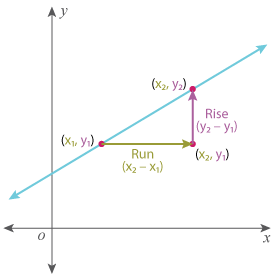
Thus, the formula for calculating the slope of a straight line is:

What Are the Types of Slope?

There are four different types of slope. Let’s learn what they are.

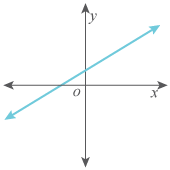
Type 1: A Positive Slope

When a line rises from left to right, it has a positive slope (m > 0).

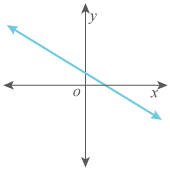
Type 2: A Negative Slope

When a line falls from left to right, it has a negative slope (m < 0).

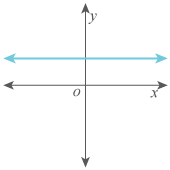
Type 3: A Zero Slope

When the line is horizontal, it has a zero slope (m = 0).

Type 4: An Undefined Slope

When the line is vertical, its slope is undefined.

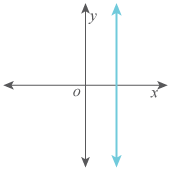
Thus the slope of a line not only measures its steepness, it also describes its direction: extending upward or downward and horizontal or vertical. The greater the slope measure is, the steeper the line is.

Mathematical and Real-World Examples of Slope

Now that we know the slope formula and its types, let’s explore some real-life instances of slope.

Example 1

Imagine you are biking uphill.

Watch the biker cycle uphill with a click!

Let’s transfer the scenario onto a Cartesian plane. The line is the hill’s outline.

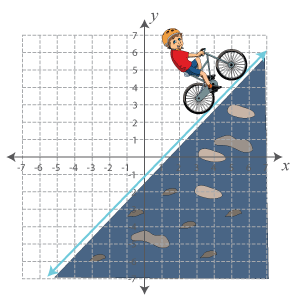
Let’s figure out how steep this hill is. We'll pick any two points on this line: A (3, 2) and B (6, 5), and find the rise and run.

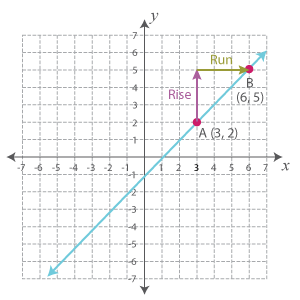
Now, the slope of the hill is:

Slope = RiseRun

⇨ m = 33

⇨ m = 1 unit

Note: A positive slope indicates an uphill movement from left to right.

How about Choosing a Different Set of Points on the Same Line?

Let’s select C (2, 1) and D (4, 3). Let’s move up and across to reach point D.

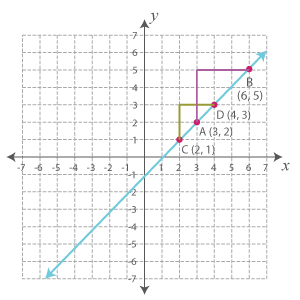
Slope = Change in yChange in x

⇨ m = 22

⇨ m = 1 unit

∴ Slope of AB = Slope of CD

Thus, the slope of a straight line is constant. Whatever points we pick, the slope remains the same.

Example 2

Imagine this snowboarder sliding downhill.

See the snowboarder slide downhill with a click!

Let’s represent that on a coordinate plane, pick two points, and determine the vertical and horizontal distances between them.

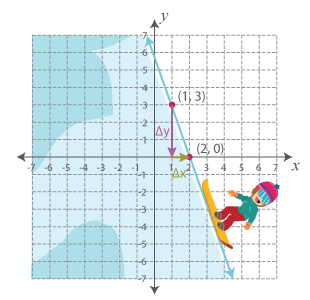
As we move downward from (1, 3), we are aligned with (2, 0). So, the change in y is negative 3 units. The change in x is a positive 1 unit. Now, the slope of the hill is:

Slope = ∆y∆x

⇨ m = –31

⇨ m = –3 units

Note: A negative slope indicates a downhill movement in the left-right direction.

Example 3

Now imagine driving on a flat road.

Steer the car with a click!

The road looks like this horizontal line that has no steepness.

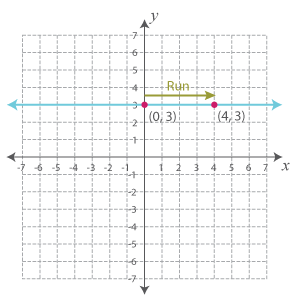
Here, the run is 4. But there’s no change in y, so our rise is 0. Now, the slope of the road is:

⇨ m = RiseRun

⇨ m = 04

⇨ m = 0

Thus, the road here is an example of zero slope.

Example 4

Let's move from no steepness to the steepest line this time. The best example that fits this scenario is an elevator.

Watch the elevator move with a click!

That’s a simple vertical line when depicted on an xy-plane.

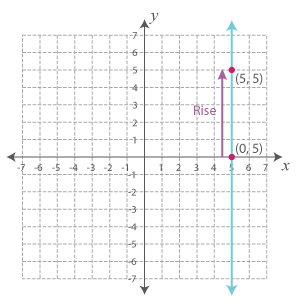
The rise is 5 units. But, there’s absolutely no movement across. Hence, the run is 0.

Slope = RiseRun

⇨ m = 50

We can’t divide 5 by 0. Thus, the slopes of such lines are undefined.

Example 5

Let’s find the slope of a line without a graph this time! We are given a line that passes through the points (1, –1) and (6, 2).

Let’s take (x₁, y₁) = (1, –1) and (x₂, y₂) = (6, 2).

Slope = y₂ – y₁x₂ – x₁

Plugging the values in the formula, we have:

m = 2 – (–1)6 – 1

Upon simplification, we get:

⇨ m = 2 + 16 – 1

⇨ m = 35

Thus, the slope is 35.

A Brisk Trot through the Lesson!

• The slope or gradient of a line measures the steepness of a line.

• There are four types of slope: positive, negative, zero, and undefined. These determine the line’s direction: increasing, decreasing, horizontal, or vertical.

• A positive gradient says that the line ascends or rises from left to right, and a negative gradient says that the line descends or falls from left to right.

• The slope of every horizontal line is 0, and the slope of every vertical line is undefined.

• The slope is constant on any point of the line.

---