Digitally Fillable Worksheets
Worksheets by Grade
Number Sense and Operations
Measurement
Statistics and Data
Geometry
Pre-Algebra
AlgebraEquation Worksheets
Access this valuable resource with purposive worksheets that focus on imparting abundant learning and practice opportunities for solving algebraic equations. Our expertly designed pdf worksheets ensure that the concepts are made explicit enough to guide the students effortlessly through the steps of finding the values of the required variables, to fulfill the condition stated.
List of Equation Worksheets
Detailed Description of Equation Worksheets
One-Step Equation Worksheets
Throw a bit of challenge to students, so that they gain considerable mastery in solving equations involving mixed operations with integers, decimals, fractions and geometrical applications.
ExploreTwo-Step Equation Worksheets
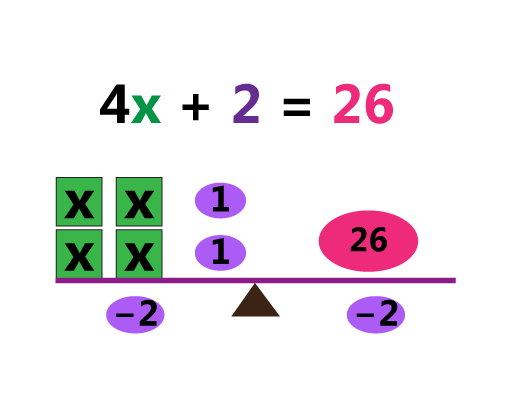
Provide learners of grade 6 and above, our set of free worksheets to acquire mastery in solving and verifying two-step equations, involving integers, decimals and fractions. If practice truly makes perfect, then remain assured of the excellence that students achieve.
ExploreMulti-Step Equation Worksheets
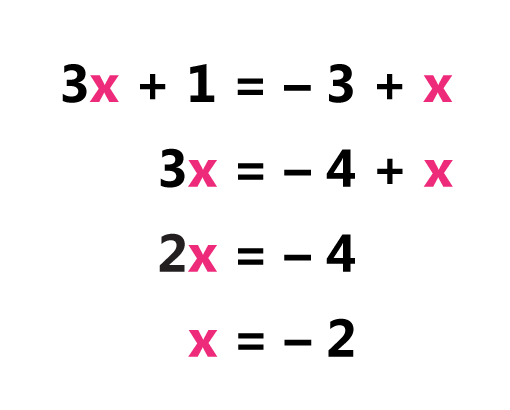
Solving and verifying multi-step equations will no longer be a daunting task for students of grades 6 and above, as our ingenious collection of printable worksheets are here to assist them at every step required to equations involving integers, decimals and fractions as coefficients.
ExploreRearranging Equation Worksheets
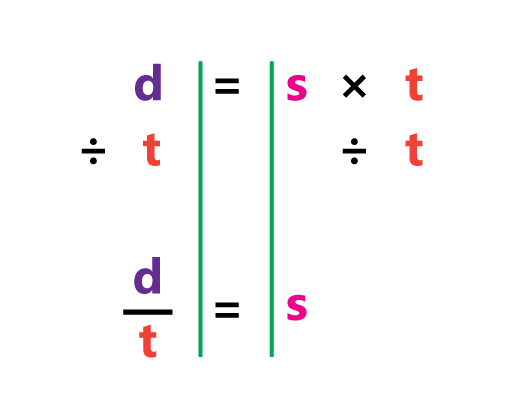
Rearranging literal equations is an essential area in solving equations by isolating the variables. Our printable exercises not only comes as a great resource to learn and practice rearranging literal equation, but also a wonderful opportunity to revise and reiterate "inverse operations" and "properties of equality".
ExploreEquation of a Line Worksheets
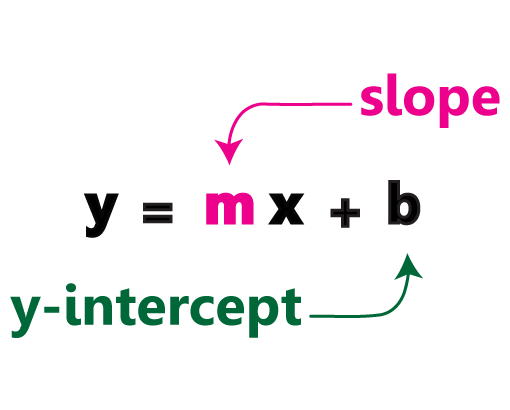
Brimming with exercises, these equation of a line pdf worksheets are a must-have for students of grade 7, grade 8, and high school to practice finding the slope, converting from one slope form to the other and much more.
ExploreSystems of Equations Worksheets
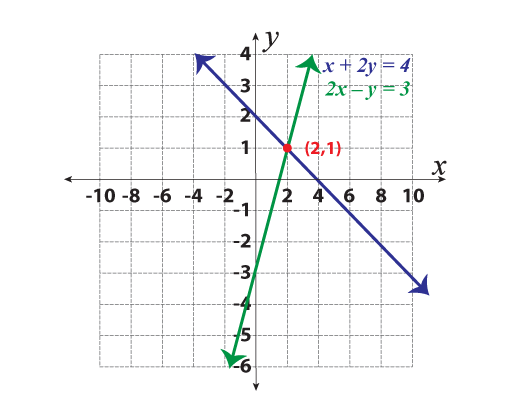
Captivate the minds of high school students to solve systems of equations using elimination method, substitution method, graphing method, and more with this set of worksheets.
Explore
